Basic FEM

by Mirza Cenanovic & Carl-Johan Jonsson

Download this page as a Matlab LiveScript

Table of contents

  1. Video Lectures
  2. Finite element method solver in 1D
    1. Weak form:
    2. Galerking approximation
    3. Iso-parametric mapping
    4. Element matrices
    5. Gauss integration
    6. Mesh
    7. Numerical Solution
  3. Visualizing the quadratic approximation
  4. L2L_2 error computation
  5. Convergence analysis

Video Lectures

Link to the playlist

Finite element method solver in 1D

Solve the following differential equation using numerical integration

−2d2ud  x2+u=x2  for  x∈[−1,5]-2\dfrac{d^2 u}{d\;x^2 }+u=x^2 \;\textrm{for}\;x\in \left\lbrack -1,5\right\rbrack d  ud  x(−1)=2,u(5)=3\dfrac{d\;u}{d\;x}\left(-1\right)=2,u\left(5\right)=3

Weak form:

2∫−15d  ud  x  d  vd  x  d  x+∫−15u  v  d  x=∫−15x2  v  d  x+2[d  ud  xv]−152\int_{-1}^5 \dfrac{d\;u}{d\;x}\;\dfrac{d\;v}{d\;x}\;d\;x+\int_{-1}^5 u\;v\;d\;x=\int_{-1}^5 x^2 \;v\;d\;x+{2\left\lbrack \dfrac{d\;u}{d\;x}v\right\rbrack }_{-1}^5

Galerking approximation

u≈φ⋅uandd  ud  x≈d  φ  d  x⋅uu\approx \boldsymbol\varphi \cdot \mathbf u \quad \text{and} \quad \frac{d\;u}{d\;x}\approx \frac{d\;{\boldsymbol\varphi }^{\;} }{d\;x}\cdot \mathbf u

Iso-parametric mapping

x(ξ)=φ  (ξ)⋅xx\left(\xi \right)={\boldsymbol\varphi }^{\;} \left(\xi \right)\cdot \mathbf x d  φ  d  x=d  φ  d  ξ  d  ξd  x=d  φ  d  ξ  J−1=d  φ  d  ξ  h−1\dfrac{d\;{\varphi }^{\;} }{d\;x}=\dfrac{d\;{\varphi }^{\;} }{d\;\xi }\;\dfrac{d\;\xi }{d\;x}=\dfrac{d\;{\varphi }^{\;} }{d\;\xi }\;J^{-1} =\dfrac{d\;{\varphi }^{\;} }{d\;\xi }\;h^{-1}

Element matrices

Se=2∫01d  φTd  ξd  φ  d  ξ1hd  ξ{\mathit{\mathbf{S} } }_e =2\int_0^1 \dfrac{d\;{\boldsymbol\varphi }^T }{d\;\xi }\dfrac{d\;{\boldsymbol\varphi }^{\;} }{d\;\xi }\dfrac{1}{h}d\;\xi Me=∫01φTφ  h dξM_e =\int_0^1 {\boldsymbol\varphi }^T \boldsymbol\varphi \; h\ d\xi fe=∫01φTx2  h  dξ=∫01φT  (φ⋅xc)2⏟x2h  dξf_e =\int_0^1 {\boldsymbol\varphi }^T x^2 \;h\;d\xi =\int_0^1 {\boldsymbol\varphi }^T \;\underset{x^2 }{\underbrace{ {\left(\boldsymbol\varphi \cdot \mathbf x_c \right)}^2 } } h\;d\xi

Gauss integration

∫01f(ξ)  d  ξ≈∑inf(ξi)wi\int_0^1 f\left(\xi \right)\;d\;\xi \approx \sum_i^n f\left(\xi_i \right)w_i

Recall: nn integration points integrate polynomials of degree 2n−12n-1 exactly!

Mesh

Draw the mesh, schematically, number the nodes, put down the boundary conditions.

Choose the approximation, i.e., element type. This defines the mesh and the basis functions as well as the Gauss integration order for the matrices.

clear
syms ue(x)
DE = -2*diff(ue,x,2) - ue == x^2;
du = diff(ue,x);

BC = [du(-1)==2, ue(5)==3];

ue = dsolve(DE, BC);

figure
fplot(ue,[-1,5], 'r', 'LineWidth',2)

Numerical Solution

Solve numerically using N quadratic elements

N = 2;
nnod = N*2+1; % Number of nodes
neq = nnod*1; % Number of equations, one degree of freedom per node
xnod = linspace(-1,5,nnod);

Visualizing the mesh

figure
plot(xnod, xnod*0, 'ok', MarkerFaceColor='k',MarkerSize=15)
text(xnod-0.03, xnod*0, cellstr(num2str([1:nnod]')), Color='w')
axis equal tight 
ylim([-0.5,0.5]); box off

Define the mesh topology, i.e., node connectivity

nodes = [(1:2:nnod-2)', (2:2:nnod-1)', (3:2:nnod)'];

Basis functions are defined here as anonymous functions. These are numeric and evaluate very fast compared to symbolic functions.

phi = @(xi)[(xi.*2.0-2.0).*(xi-1.0./2.0),xi.*(xi-1.0).*-4.0,xi.*(xi-1.0./2.0).*2.0];
dphi = @(xi)[xi.*4.0-3.0,xi.*-8.0+4.0,xi.*4.0-1.0];

The Gauss order is choosen, here, it is choosen by the highest polynomial order in the differential equation.

order = 4;
[gp, gw] = gauss(order, 0, 1);

We pre-allocate variables to their final sizes, this is done for execution performance. There are faster methods of doing this, but for readability, we will stick to this. Ask Mirza if interested for more info on performance optimization. 

S = zeros(neq,neq);
M = S; 
F = zeros(neq,1);

The main assembly loop. The heart of any FEM solver. We are looping over all elements to compute the element stiffness, mass and load matrices.

The internal loop is the Gauss integration loop.

Se=∑i42d  φ(ξi)Td  ξd  φ(ξi)d  ξ1hdξ⏟=1  wiS_e =\sum_i^4 2\dfrac{d\;{\boldsymbol\varphi \left(\xi_i \right)}^T }{d\;\xi }\dfrac{d\;\boldsymbol\varphi \left(\xi_i \right)}{d\;\xi }\dfrac{1}{h}\underset{=1}{\underbrace{d\xi } } \;w_i

remember dξd\xi is the length (or size) of the parameter space!

Me=∑i4φ(ξi)Tφ(ξi)  h  wiM_e =\sum_i^4 {\boldsymbol\varphi \left(\xi_i \right)}^T \boldsymbol\varphi \left(\xi_i \right)\;h\;w_i fe=∑i4φ(ξi)Tx(ξi)  h  wif_e =\sum_i^4 {\boldsymbol \varphi \left(\xi_i \right)}^T x\left(\xi_i \right)\;h\;w_i

where

x(ξi)=φ(ξi)⋅x=quadratic  basis  functions[φ1(ξi)φ2(ξi)φ2(ξi)]⋅[x1x2x3]x\left(\xi_i \right)= \boldsymbol \varphi \left(\xi_i \right)\cdot \mathbf x \overset{\textrm{quadratic}\;\textrm{basis}\;\textrm{functions} }{=} \left\lbrack \begin{array}{ccc} \varphi_1 \left(\xi_i \right) & \varphi_2 \left(\xi_i \right) & \varphi_2 \left(\xi_i \right) \end{array}\right\rbrack \cdot \left\lbrack \begin{array}{c} x_1 \\ x_2 \\ x_3 \end{array}\right\rbrack 
for iel = 1:N
    inod = nodes(iel,:);
    xc = xnod(inod);
    h = xc(end)-xc(1);
    Se = zeros(3,3);
    Me = Se;
    fe = zeros(3,1);
    for ig = 1:length(gp)
        xi = gp(ig);
        iw = gw(ig);
        
        Se = Se + 2*dphi(xi)'*dphi(xi)*1/h*1*iw;
        Me = Me + phi(xi)'*phi(xi)*h*1*iw;

        x = phi(xi)*xc';
        fe = fe + phi(xi)' * x^2 * h * 1 * iw;
    end
    % Assembly
    S(inod,inod) = S(inod, inod) + Se;
    M(inod,inod) = M(inod, inod) + Me;
    F(inod) = F(inod) + fe;
end
S = S-M;

Boundary conditions

d  ud  x(−1)=2,u(5)=3\dfrac{d\;u}{d\;x}\left(-1\right)=2,u\left(5\right)=3 2[d  ud  xv]−15=2d  ud  x(5)v(5)⏞gend⏟0−2d  ud  x(−1)⏟2v(−1)⏞gstart{2\left\lbrack \dfrac{d\;u}{d\;x}v\right\rbrack }_{-1}^5 =\underset{0}{\underbrace{\overset{g_{\textrm{end} } }{\overbrace{2\dfrac{d\;u}{d\;x}\left(5\right)v\left(5\right)} } } } -\overset{g_{\textrm{start} } }{\overbrace{2\underset{2}{\underbrace{\dfrac{d\;u}{d\;x}\left(-1\right)} } v\left(-1\right)} } 
g = zeros(neq,1);
g(1) = -2*2;

alldofs = 1:neq;
presc = alldofs(end); %u is known in the last degree of freedom
u = zeros(neq,1); %Pre-allocate
u(presc) = 3; %prescribe
free  = setdiff(alldofs,presc);

Modify the right hand side, e.g., 

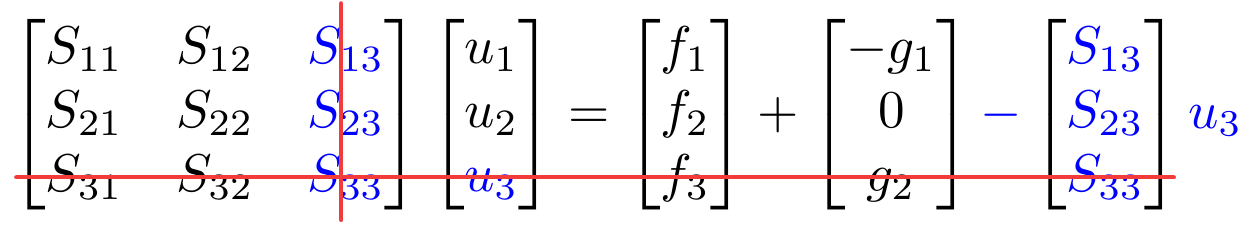
F = F + g - S(:, presc)*u(presc);

Reduce the system and solve 

u(free) = S(free,free)\F(free);
figure
fplot(ue,[-1,5], 'r', 'LineWidth',2)
hold on
plot(xnod, u, 'bo')

The blue dots represent the solution variables.

Visualizing the quadratic approximation

Every quadratic element is defined by three nodal values and in between we need to interpolate using the quadratic basis functions.

For every element ee the approximation is given by:

ue(ξ)=φ(ξ)⋅[u1u2u3]u_e \left(\xi \right)= \boldsymbol\varphi \left(\xi \right) \cdot \left\lbrack \begin{array}{c} u_1 \\ u_2 \\ u_3 \end{array}\right\rbrack 
figure
fplot(ue,[-1,5], 'r', 'LineWidth',2)
hold on
plot(xnod, u, 'bo')

We will let ξ\xi be a set of n=100n=100 evenly spaced numbers between 0 and 1.

for iel = 1:N
    iel
    inod = nodes(iel,:);
    xc = xnod(inod);
    U = u(inod);
    xi = linspace(0,1,100)';
    
    Ue = phi(xi)*U;
    Xe = phi(xi)*xc';
    plot(Xe,Ue,'-')
end
title("Two quadratic elements")

L2L_2 error computation

L2error:=∫Ω  (U−u)2  d  xL_2 \textrm{error}:=\sqrt{\int_{\Omega }^{\;} {\left(U-u\right)}^2 \;d\;x}

Now we want to compute the difference between the function for each element and adding it all up.

L2error:=∫Ω  (U−u)2  d  x=∑eN∫e  (Ue−u)2  d  xL_2 \textrm{error}:=\sqrt{\int_{\Omega }^{\;} {\left(U-u\right)}^2 \;d\;x}=\sqrt{\sum_e^N \int_e^{\;} {\left(U_e -u\right)}^2 \;d\;x}

where

Ue(x)=φ(x)ue=lin  ele[φ1φ1][u1u2]U_e \left(x\right)=\varphi \left(x\right){\mathit{\mathbf{u} } }_e \overset{\textrm{lin}\;\textrm{ele} }{=} \left\lbrack \begin{array}{cc} \varphi_1 & \varphi_1 \end{array}\right\rbrack \left\lbrack \begin{array}{c} u_1 \\ u_2 \end{array}\right\rbrack

remember: x(ξ)=φ  (ξ)⋅xx\left(\xi \right)={\varphi }^{\;} \left(\xi \right)\cdot x

ue = matlabFunction(ue);

L2err = 0;
for iel = 1:N
    inod = nodes(iel,:);
    xc = xnod(inod);
    h = xc(end)-xc(1);
    U = u(inod);
    err = 0;
    for ig = 1:length(gp)
        xi = gp(ig);
        iw = gw(ig);
        x = phi(xi)*xc';
        Ue = phi(xi)*U;
        err = err + (ue(x)-Ue)^2 * h * 1 * iw;
    end
    L2err = L2err + err;
end
L2err = sqrt(L2err)
L2err = 9.4298

Convergence analysis

We shall now compute the L2L_2 error for N={2,4,8,16,32}N=\left\lbrace 2,4,8,16,32\right\rbrace elements and plot the convergence.

clear

syms ue(x)
DE = -2*diff(ue,x,2) - ue == x^2;
du = diff(ue,x);
BC = [du(-1)==2, ue(5)==3];
ue = dsolve(DE, BC);

NN = [2,4,8,16,32,64,128];
L2Err1 = []; Time1 = []; XX1 = [];
L2Err2 = []; Time2 = []; XX2 = [];

To keep the code somewhat clean, we shall move the whole solver code into a function called FEM1DLinSolver.

for N = NN
    tic
    [u,L2err,h,xnod] = MyKickassQuadSolver(N,ue);
    Time1(end+1) = toc;
    L2Err1(end+1) = L2err;
    XX1(end+1)=h;
    
    figure(1); clf; hold on
    fplot(ue,[-1,5],'r')
    plot(xnod,u,'bo')
    title(sprintf("%d quadratic elements",N))

    tic
    [u,L2err,h,xnod] = MyKickassLinSolver(N,ue);
    Time2(end+1) = toc;
    L2Err2(end+1) = L2err;
    XX2(end+1)=h;

    figure(2); clf; hold on
    fplot(ue,[-1,5],'r')
    plot(xnod,u,'bo-')
    title(sprintf("%d linear elements",N))
end

figure; hold on
plot(NN,L2Err1,'-ro','DisplayName','Quadratic Approximation')
plot(NN,L2Err2,'-bs','DisplayName','Linear Approximation')
set(gca,'XScale','log','YScale','log')
grid on
xticks(NN)
axis equal
xlabel("Number of elements"); ylabel("L_2 error")
legend("show","Location","southwest")

Not only is the quadratic approximation better for every number of elements, it also converges faster than the linear approximation.

Note that evaluating runtime for these small problems is tricky, a definitive comparison can only be seen with a high number of elements, since the overhead of the computations is significant when we have a small number of elements.

It makes more sense to plot the number of degrees of freedom than number of elements.

To do a proper convergence analysis we shall plot the errors vs the mesh size, rather than number of degrees of freedom or number of elements. We can then compute the slope of the convergence graph, which is the rate of convergence. It can be mathematically shown what convergence rate we can expect from a certain interpolant using error estimation.

To compute the convergence rate, we can do a numerical convergence study by computing a number of L2L_2 errors, each time doubling the number of elements. The convergence rate is then given by

p:=Δlog⁡(L2error)Δlog⁡(h) p:=\dfrac{\Delta \log(L_2\textrm{error}) }{\Delta \log(h) }

where hh is the mesh size.

The slope of the error convergence for the quadratic approximation tends towards 3 and for the linear approximation towards 2.

diff(log(L2Err1))./diff(log(XX1))
ans = 1x6    
    3.2776    3.4207    3.1950    3.0607    3.0162    3.0041
diff(log(L2Err2))./diff(log(XX2))
ans = 1x6    
    0.9803    1.5597    1.8643    1.9639    1.9908    1.9977

function [u,L2err,h,xnod] = MyKickassQuadSolver(N,ue)

nnod = N*2+1;
xnod = linspace(-1,5,nnod);

nodes = [(1:2:nnod-2)', (2:2:nnod-1)', (3:2:nnod)'];

neq = nnod*1;

phi = @(xi)[(xi.*2.0-2.0).*(xi-1.0./2.0),xi.*(xi-1.0).*-4.0,xi.*(xi-1.0./2.0).*2.0];

dphi = @(xi)[xi.*4.0-3.0,xi.*-8.0+4.0,xi.*4.0-1.0];

order = 4;
[gp, gw] = gauss(order, 0, 1);

S = zeros(neq,neq);
M = S; 
F = zeros(neq,1);
for iel = 1:N
    inod = nodes(iel,:);
    xc = xnod(inod);
    h = xc(end)-xc(1);
    Se = zeros(3,3);
    Me = Se;
    fe = zeros(3,1);
    for ig = 1:length(gp)
        xi = gp(ig);
        iw = gw(ig);
        
        Se = Se + 2*dphi(xi)'*dphi(xi)*1/h*1*iw;
        Me = Me + phi(xi)'*phi(xi)*h*1*iw;

        x = phi(xi)*xc';
        fe = fe + phi(xi)' * x^2 * h * 1 * iw;
    end

    % Assembly
    S(inod,inod) = S(inod, inod) + Se;
    M(inod,inod) = M(inod, inod) + Me;
    F(inod) = F(inod) + fe;
end

S = S-M;

g = zeros(neq,1);
g(1) = -2*2;

alldofs = 1:neq;
presc = alldofs(end);
u = zeros(neq,1);
u(presc) = 3;
free  = setdiff(alldofs,presc);

F = F + g - S(:, presc)*u(presc);

u(free) = S(free,free)\F(free);

ue = matlabFunction(ue);
L2err = 0;
for iel = 1:N
    inod = nodes(iel,:);
    xc = xnod(inod);
    h = xc(end)-xc(1);
    U = u(inod);
    err = 0;
    for ig = 1:length(gp)
        xi = gp(ig);
        iw = gw(ig);
        x = phi(xi)*xc';
        Ue = phi(xi)*U;
        err = err + (ue(x)-Ue)^2 * h * 1 * iw;
    end
    L2err = L2err + err;
end
L2err = sqrt(L2err);

end

function [u,L2err,h, xnod] = MyKickassLinSolver(N,ue)

xnod = linspace(-1,5,N+1);
nodes = [(1:N)', (2:N+1)'];
nnod = length(xnod);
neq = nnod*1;

phi = @(xi)[1-xi, xi];
dphi = [-1, 1];

order = 2;
[gp, gw] = gauss(order, 0, 1);

S = zeros(neq,neq);
M = S; 
F = zeros(neq,1);
for iel = 1:N
    inod = nodes(iel,:);
    xc = xnod(inod);
    h = xc(end)-xc(1);
    Se = zeros(2,2);
    Me = Se;
    fe = zeros(2,1);
    for ig = 1:length(gp)
        xi = gp(ig);
        iw = gw(ig);
        
        Se = Se + 2*dphi'*dphi*1/h*1*iw;
        Me = Me + phi(xi)'*phi(xi)*h*1*iw;

        x = phi(xi)*xc';
        fe = fe + phi(xi)' * x^2 * h * 1 * iw;
    end

    % Assembly
    S(inod,inod) = S(inod, inod) + Se;
    M(inod,inod) = M(inod, inod) + Me;
    F(inod) = F(inod) + fe;
end

S = S-M;

g = zeros(neq,1);
g(1) = -2*2;

alldofs = 1:neq;
presc = alldofs(end);
u = zeros(neq,1);
u(presc) = 3;
free  = setdiff(alldofs,presc);

F = F + g - S(:, presc)*u(presc);

u(free) = S(free,free)\F(free);

ue = matlabFunction(ue);
L2err = 0;
for iel = 1:N
    inod = nodes(iel,:);
    xc = xnod(inod);
    h = xc(end)-xc(1);
    U = u(inod);
    err = 0;
    for ig = 1:length(gp)
        xi = gp(ig);
        iw = gw(ig);
        x = phi(xi)*xc';
        Ue = phi(xi)*U;
        err = err + (ue(x)-Ue)^2 * h * 1 * iw;
    end
    L2err = L2err + err;
end
L2err = sqrt(L2err);
end

function [x, w, A] = gauss(n, a, b)
    
    %------------------------------------------------------------------------------
    % gauss.m
    %------------------------------------------------------------------------------
    %
    % Purpose:
    %
    % Generates abscissas and weigths on I = [ a, b ] (for Gaussian quadrature).
    %
    %
    % Syntax:
    %
    % [x, w, A] = gauss(n, a, b);
    %
    %
    % Input:
    %
    % n    integer    Number of quadrature points.
    % a    real       Left endpoint of interval.
    % b    real       Right endpoint of interval.
    %
    %
    % Output:
    %
    % x    real       Quadrature points.
    % w    real       Weigths.
    % A    real       Area of domain.
    %------------------------------------------------------------------------------
    
    
    % 3-term recurrence coefficients:
    n = 1:(n - 1);
    beta = 1 ./ sqrt(4 - 1 ./ (n .* n));
    
    % Jacobi matrix:
    J = diag(beta, 1) + diag(beta, -1); 
    
    
    % Eigenvalue decomposition:
    
    %
    % e-values are used for abscissas, whereas e-vectors determine weights.
    %
    
    [V, D] = eig(J);
    x = diag(D);
    
    
    % Size of domain:
    A = b - a;
    
    
    % Change of interval:
    
    %
    % Initally we have I0 = [ -1, 1 ]; now one gets I = [ a, b ] instead.
    %
    % The abscissas are Legendre points.
    %
    
    if ~(a == -1 && b == 1)
      x = 0.5 * A * x + 0.5 * (b + a);
    end
    
    
    % Weigths:
    w = V(1, :) .* V(1, :);
    w = w';
    x=x';
end

© Mirza Cenanovic. Last modified: December 21, 2023. Website built with Franklin.jl and the Julia programming language.